CLEARSY has developed a system formal verification for the CBTC of New York subway line 7, using the B method. The obtained formal system verification is an element for the safety assessment of this critical railway system.
- CLIENT : New York City Transit (NYCT)
- SITE : New York – USA
- DATE : 2011 to 2013
Context
In its process of railroad network modernization New York City Transit has awarded THALES Toronto for the design and fitting of a CBTC system for the subway line 7 (Flushing).
This system will safely improve the trains’ movements by reducing the headway, thus improving the transportation capacity with an additional benefit in reducing the required wayside equipment (signals and track circuits).
The CBTC system is composed of an on-board computer (fitted in renewed R142 cars) and of filed and office equipment (zone controllers and central supervision). It interfaces to the existing interlocking system (adapted with specific modifications).
CLEARSY’s Task
NYCT has decided to obtain a mathematical proof-based safety guaranty for the Flushing new CBTC. To achieve this system formal verification, CLEARSY conducted a system level proof based on the B formal language and the Atelier B toolkit.
The proven target properties are:
- Impossibility of collision between trains
- Impossibility of derailment over an unlocked switch
- Impossibility of over-speeding
Our actions
CLEARSY in its process made use of the detailed design and algorithm description documents from THALES for the Flushing CBTC. For instance, we made use of the following details:
- Pulse counting from tachometers (and specific points about direction change or slipping)
- Kalman filters for the speed measurement
- How gradients are used in the safe braking model
- Wayside to on-board communication: messages worst case dating, messages crossings, timeouts
- Train tracking: exchange of unequipped train suspicion between zone controllers
- Possible signal overruns (manual trains), associated locking including provisions for returns or mode changes
- Routes cancel and possible race conditions in the wired interface between CBTC and interlocking..
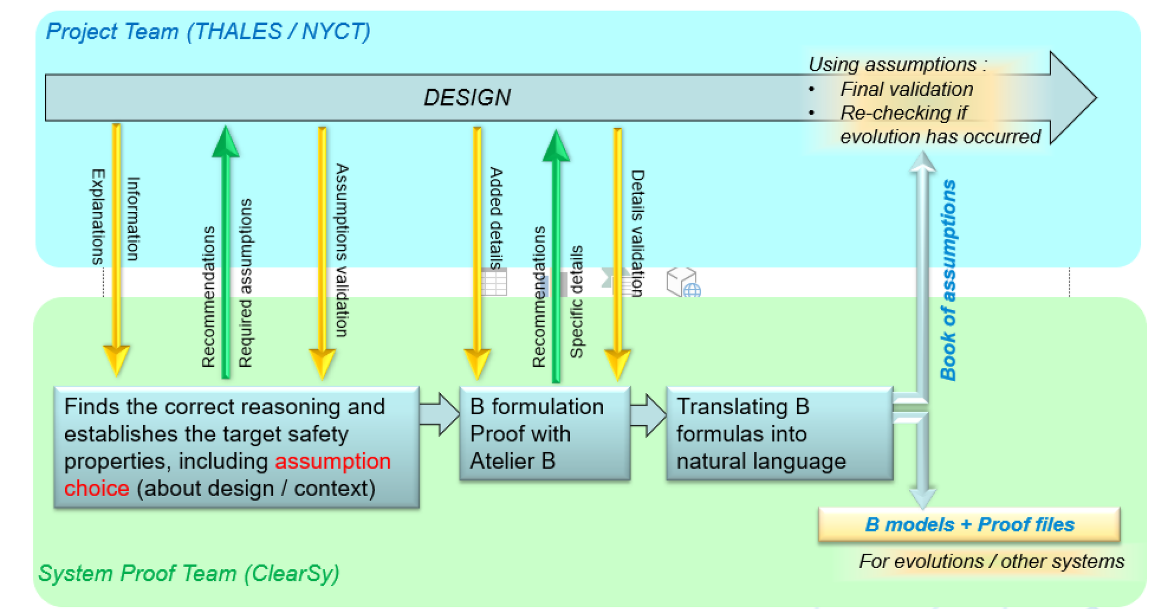
The B models contain the mathematical formulation of target properties, the mathematical formulation of all necessary assumptions and some elements required to pilot the proof. Once these B models are proved using Atelier B, we obtained the guaranty that all target properties could be mathematically deduced from the chosen assumptions.
So those assumptions are a set of properties sufficient to mathematically guarantee the target safety properties. Those assumptions relates to the design, the hardware or the context: all conditions that are not purely mathematical rules must be expressed for the Atelier B’s automatic prover to succeed.
Those assumptions have been defined and decided in an on-going manner during the project, together with NYCT and THALES, thus leading to realistic assumptions matching the design and thus interacting with the design process (using recommendations).
At the end of this project, we started from the B formulas denoting these assumptions to reach a very precise natural language redaction of each assumption. Thus, the assumptions can be re-validated before the actual CBTC commissioning and they remain re-checkable in any case of change or evolution. So we delivered at set of detailed and validated documents describing in an easy-to-understand way all sufficient conditions so that the target properties are mathematically guaranteed.
For software parts, these assumptions define precise condition that each software part should establish. So the system level proof produces some precise safety validation conditions for the software, while remaining independent from the detailed software design.
To summarize, this project implements the principle that a mathematical proof for the safety properties of a system (whatever its size) can be obtained while the system is designed, with a level of detail determined by the chosen assumptions. Please note that this process requires a fine understanding of the “true why” the design actually ensures the safety, thus requiring strong interactions with the domain experts. But such interactions between domain experts and people responsible for finding a mathematical proof have a lot of benefits by themselves.
Link to this référence
Linked to this référence
Link to this référence